Basic principle of this experiment
The determination of the plateau in a Geiger-Müller (GM) counter involves studying the behavior of the counter’s detection efficiency and stability over a range of applied voltages. The basic principles of this lab experiment are as follows:
1. Purpose and Introduction:
- Explain the goal of the experiment: to determine the voltage range at which the GM counter operates efficiently and stably, known as the plateau.
- Briefly introduce the GM counter’s function as a radiation detector based on ionization.
2. Variation of Voltage:
- Describe the experimental setup, including the GM counter, radiation source (if applicable), and voltage supply.
- Explain that the voltage applied to the GM counter is varied systematically across a range.
3. Counting Rate Measurement:
- Discuss how the counting rate of the GM counter is measured at each voltage level.
- Mention the use of a radiation source emitting radiation (such as alpha, beta, or gamma) that the GM counter can detect.
4. Data Collection and Analysis:
- Explain that data is collected by recording the counting rate at each voltage setting.
- Describe how the data is plotted in a graph, with voltage on the x-axis and counting rate on the y-axis.
5. Plateau Region Identification:
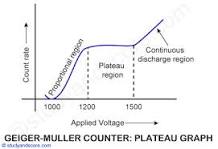
- Define the plateau region as the range of voltages where the counting rate remains relatively constant.
- Explain that outside the plateau region, the counting rate might exhibit sudden increases or decreases.
6. Voltage Selection:
- Emphasize the significance of operating the GM counter within the plateau region for accurate radiation detection.
- Discuss how selecting the appropriate operating voltage ensures stable and consistent detection efficiency.
7. Plateau Characteristics:
- Mention that the plateau indicates a region where the GM counter’s gas amplification mechanism is operating uniformly.
- Explain that within the plateau, the avalanche of electrons created by ionization is stable and efficient.
8. Significance and Applications:
- Discuss the importance of determining the plateau in using GM counters for radiation detection in various fields, including radiation monitoring, health physics, and research.
9. Limitations and Error Sources:
- Mention potential sources of error, such as background radiation interference or variations in the radiation source intensity.
10. Conclusion: - Summarize the experiment’s outcomes: the identification of the plateau region and its significance. - Emphasize the practical implications of understanding the plateau for accurate and reliable GM counter measurements.
In summary, the basic principles of determining the plateau in a Geiger-Müller counter lab experiment involve varying the applied voltage, measuring the counting rate, identifying the plateau region, and understanding its significance for the counter’s efficiency and stability in detecting ionizing radiation.
Main principal of this experiment
The determination of the plateau in a Geiger-Müller (GM) counter is a crucial aspect of laboratory experiments involving radiation detection. The plateau region refers to a range of operating voltages where the GM counter exhibits consistent and reliable behavior. Here are the main principles involved in determining the plateau of a Geiger-Müller counter in a lab experiment:
-
Stable Operating Conditions: The GM counter is operated under controlled conditions, including a stable radiation source and a specific gas mixture inside the counter’s tube. The goal is to ensure consistent and repeatable results.
-
Variation of Voltage: The experiment involves systematically varying the voltage applied to the GM counter over a certain range. This is done by adjusting the voltage supply to the counter.
-
Counting Rate Measurement: At each voltage setting, the counting rate of the GM counter is measured. The counting rate refers to the number of electrical pulses or signals detected by the counter per unit time. This is typically measured in counts per second (cps) or counts per minute (cpm).
-
Data Collection and Plotting: The measured counting rates are recorded for each voltage setting. A graph is then created with voltage on the x-axis and the corresponding counting rate on the y-axis.
-
Plateau Region Identification: The plateau region is identified on the graph as the voltage range where the counting rate remains relatively constant or exhibits only a slight increase. This region represents the range of operating voltages where the GM counter is working efficiently and provides consistent results.
-
Voltage Range Determination: The voltage range of the plateau is typically determined by selecting the points on the graph where the counting rate deviates by a certain percentage (e.g., ±10%) from the maximum or average counting rate.
-
Optimal Operating Voltage: The optimal operating voltage of the GM counter is often taken as the midpoint of the plateau region. This voltage setting ensures stability, efficiency, and reliability in radiation detection.
-
Importance and Implications: The determination of the plateau and optimal operating voltage is critical for accurate radiation measurements. It ensures that the GM counter functions within a reliable range, avoiding unwanted effects like excessive dead time or saturation.
-
Applications and Future Considerations: Discuss the practical applications of the determined optimal voltage in radiation detection scenarios. Also, suggest potential improvements or extensions of the experiment, such as exploring different gas mixtures or radiation sources.
In summary, the main principles of determining the plateau of a Geiger-Müller counter in a lab experiment involve systematically varying the voltage, measuring counting rates, plotting data, identifying the stable plateau region, and determining the optimal operating voltage for accurate and efficient radiation detection.
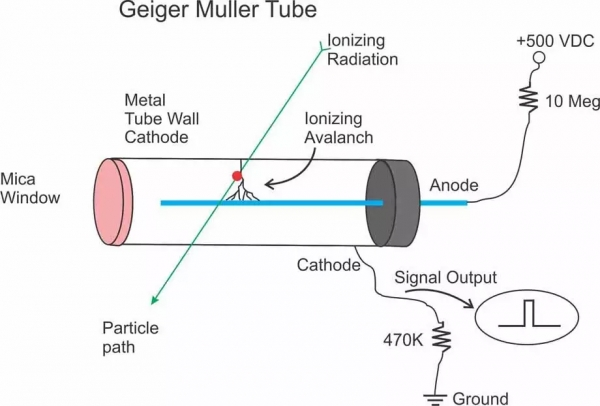
Principle of Working of GM Counter
The ionizing particle passing through the tube ionizes the gas and electrons so produced move towards Anode. The velocity is quite high and they later produce secondary electrons after repeated collisions with the particles of the gas. These secondary electrons further produce more electrons in Geometric progression.
Due to this large multiplication action, a large ionization current is produced.
Advantages of GM Counter
-
It can count alpha, beta, gamma particles as well as cosmic rays.
-
It has high sensitivity.
-
Power supply need not be precisely regulated as the pulse height is constant over a large range.
-
Because of the fact that output pulse is very high, so the Amplification needed is also very subtle.
Disadvantages of GM Counter
-
Energies cannot be measured by it as it has a lack of differentiating abilities.
-
It cannot detect uncharged particles like Neutrons.
-
It is less efficient due to the large paralysis time limits and large dead time.
-
Quenching agent used in this counter often decomposes, leading to less lifetime of the GM Counter.
whats are anode & cathode & pressure difference
In a Geiger-Müller (GM) counter, the anode and cathode are two crucial components that play essential roles in the detection of ionizing radiation. Additionally, the pressure difference within the counter’s gas-filled tube is significant for its proper functioning. Here’s an explanation of these terms:
-
Anode and Cathode:
- Anode: The anode is a positively charged electrode within the GM counter’s gas-filled tube. It typically consists of a metal wire or plate located at the center of the tube. The anode collects the free electrons generated during the ionization process.
- Cathode: The cathode is a negatively charged electrode within the GM counter’s gas-filled tube. It’s usually the outer metal casing of the tube. The cathode establishes the electric field that accelerates the free electrons towards the anode after they are created by ionization.
-
Pressure Difference:
- In a GM counter, the gas-filled tube contains a low-pressure gas, often a mixture of inert gases or quenching gases.
- The pressure difference between the inside of the tube and the surrounding environment is crucial for controlling the electric field and the detection process.
- A low gas pressure is maintained to prevent spontaneous discharges and ensure that each radiation interaction generates a distinct and measurable pulse.
- The low-pressure gas allows for efficient electron multiplication (avalanche) near the anode, leading to the generation of detectable electrical signals.
The pressure difference and the arrangement of the anode and cathode create the necessary conditions for the ionization process and the subsequent detection of ionizing radiation. When ionizing radiation enters the GM counter’s gas-filled tube, it ionizes the gas atoms, creating free electrons and positively charged ions. The electric field between the anode and cathode accelerates the free electrons towards the anode, creating an electron avalanche. The resulting electrical pulse is detected, amplified, and recorded, allowing the GM counter to quantify the presence and intensity of ionizing radiation.
In summary, the anode and cathode, along with the maintained pressure difference within the gas-filled tube, create the necessary conditions for the ionization process and the generation of detectable electrical pulses in a Geiger-Müller counter.
Quenching gas & mechanism
Quenching gas refers to a type of gas introduced into radiation detection devices, such as Geiger-Müller counters or scintillation detectors, to limit or “quench” the duration of the electrical pulses generated during the detection process. The primary purpose of using quenching gas is to prevent prolonged ionization and to prepare the detector for the next event, ensuring accurate and efficient radiation detection. Quenching gases are often added to inert gases within the detection device’s detection chamber.
In a Geiger-Müller (GM) counter, for instance, the quenching gas serves several important functions:
-
Recovery Time: After an ionization event and the subsequent electron avalanche, the detector needs to be reset for the next event. Quenching gases help the detector return to its non-conductive state quickly, reducing the recovery or “dead” time between successive radiation events.
-
Preventing Afterpulses: Afterpulses are secondary electrical pulses that can be generated in the detector due to delayed ionization or recombination processes. Quenching gases can help suppress or minimize the occurrence of afterpulses by rapidly neutralizing any residual ions and electrons from the previous event.
-
Enhancing Accuracy: Quenching gases contribute to maintaining a consistent and reliable response of the detector to radiation events. By reducing the duration of the pulses, the detector becomes more sensitive to the timing and characteristics of individual events, leading to more accurate radiation measurements.
-
Extending Detector Lifespan: Prolonged ionization or afterpulses can potentially damage the detector’s sensitive components over time. Quenching gases help prevent excessive ionization, thus extending the operational lifespan of the detector.
Commonly used quenching gases include methane (CH4), isobutane (C4H10), and ethylene (C2H4). These gases have properties that facilitate rapid recombination of ions and electrons, effectively stopping ionization and reducing the duration of the electrical pulses generated during the detection process.
Overall, quenching gases are crucial in maintaining the efficiency, accuracy, and durability of radiation detection devices by ensuring prompt recovery, minimizing afterpulses, and enhancing the overall performance of the detector.
what is counted by counter
Inert Gas and ionizations
In a Geiger-Müller (GM) counter, the inert gas used is typically helium or argon, often in a mixture with a small percentage of another gas, such as halogens like neon or quenching gases like methane or isobutane. The choice of gas mixture depends on the specific application and the type of radiation being detected. The gas-filled tube is a crucial component of the GM counter, as it plays a fundamental role in the ionization process that enables radiation detection.
Ionization Process in GM Counter: The primary mechanism of radiation detection in a GM counter relies on the ionization of gas atoms by incoming ionizing radiation. When high-energy radiation, such as alpha, beta, or gamma radiation, enters the GM tube filled with the inert gas mixture, it interacts with the gas atoms in several ways:
-
Alpha Particles: These are heavy, positively charged particles. When an alpha particle enters the gas-filled tube, it collides with the gas atoms, causing intense ionization. It can strip multiple electrons from the gas atoms along its path, creating many ion pairs.
-
Beta Particles: These are high-energy electrons or positrons. When a beta particle enters the gas, it also ionizes the gas atoms through collision, although the ionization is less intense compared to alpha particles.
-
Gamma Rays: These are high-energy photons. Gamma rays interact with the gas through the photoelectric effect and Compton scattering. In the photoelectric effect, a gamma ray photon ejects an inner-shell electron from a gas atom, creating an ion pair. In Compton scattering, the gamma ray transfers energy and momentum to an electron, causing it to be ejected and creating an ion pair.
-
Ionization and Electron Avalanche: Regardless of the type of ionizing radiation, the initial ionization event creates free electrons and positively charged ions in the gas. Due to the high voltage applied between the anode and cathode, the free electrons are accelerated towards the anode (positively charged) and gain enough kinetic energy to ionize more gas atoms through collision. This creates a chain reaction, leading to an “electron avalanche.”
-
Current Pulse: As the electron avalanche reaches the anode, a sudden burst of current flows through the circuit. This current pulse is the detected signal that indicates the presence of ionizing radiation.
-
Gas Quenching: After each avalanche, the gas needs to be quenched or brought back to a non-conductive state to prepare for the next event. This is typically achieved by adding quenching gases to prevent prolonged ionization.
In summary, inert gases like helium or argon play a crucial role in facilitating the ionization process within the GM counter. The ionization of gas atoms by incoming ionizing radiation leads to electron avalanches and the generation of detectable current pulses, allowing the GM counter to effectively detect and quantify ionizing radiation.